Музыкальный редактор CubaseSX
Иллюстрация процесса квантования
Рисунок 1.8. Иллюстрация процесса квантования сигнала (интерполяция нулевого порядка)
В теоретических работах для представления дискретных сигналов используют функцию отсчетов (дельта-функцию) — бесконечно большой по амплитуде и бесконечно короткий по времени импульс. Площадь дельта-функции равна единице. Разумеется, функции отсчетов в природе не существуют. На практике они заменяются прямоугольными импульсами малой длительности.
Если взять последовательность смещенных во времени функций отсчетов и умножить ее на ординаты кривой линии, соответствующей аналоговому сигналу, то получится дискретный по времени сигнал, который можно представить графически так, как показано на Рисунок 1.8, в. В данном случае это и есть шум квантования, представленный дискретными отсчетами.
Не существует и идеальных фильтров, с помощью которых можно было бы точь-в-точь восстановить аналоговый сигнал по его дискретным значениям. Однако в современных АЦП используются методы, позволяющие свести погрешности, обусловленные неидеальностью преобразования, к разумному минимуму.
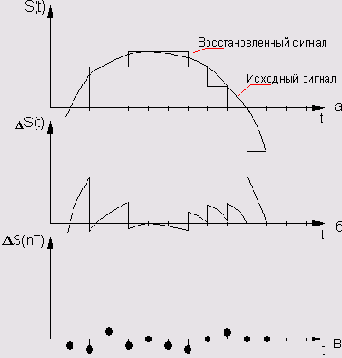
На Рисунок 1.9, а показан исходный аналоговый сигнал и сигнал, восстановленный из цифрового с использованием интерполяции 1-го порядка (отсчеты соединяются отрезками прямых линий).
Видно, что разница между исходным и восстановленным сигналом (Рисунок 1.9, б) гораздо меньше, чем при использовании интерполяции нулевого порядка (Рисунок 1.8, а). А ведь в современных ЦАП используются гораздо более сложные алгоритмы восстановления аналогового сигнала.
Что касается цифрового шума квантования (Рисунок 1.8, в), бесспорно, при цифроаналоговом преобразовании он трансформируется в некий аналоговый шум. Вид этого шумового колебания будет зависеть от конкретного
АЦП, но его уровень будет гораздо меньше, чем уровень шумового процесса, показанного на Рисунок 1.8, б.
Распространенная среди сторонников аналогового звука страшилка "Результат дискретизации ужасно отличается от исходного сигнала" основана именно на неадекватном представлении шума квантования (Рисунок 1.8, б).