Классический спектр

Начать разбираться в сущности спектральных представлений лучше с разложения в ряд Фурье периодического сигнала. Всякая периодическая функция (с ограничениями, носящими абстрактный характер) может быть представлена в виде разложения в ряд по тригонометрическим функциям

(1.1)

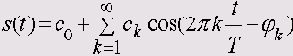
Таким образом, периодическая функция s(t) представлена суммой слагаемых, каждое из которых есть не что иное, как косинусоидальное колебание с амплитудой сk и начальной фазой

.
Совокупность коэффициентов сk называется амплитудным спектром сигнала, а

— фазовым спектром.
Частоты всех синусоидальных колебаний, из которых составляется периодическая функция s(t), кратны основной частоте F =1/Т. Отдельные составляющие называются гармониками. Колебание с частотой F называется первой гармоникой (k = 1), с частотой 2F— второй гармоникой (k = 2) и т. д.
Ряд Фурье дает разложение периодической функции по тригонометрическим функциям. Это разложение можно применить и к непериодической функции, которую рассматривают как предельный случай периодической функции при неограниченном возрастании периода.
Если Т->

, то F-> df, a 2pk/T-> w (параметр w— круговая текущая частота, изменяющаяся непрерывно). Не хотелось бы здесь рассказывать подробно обо всех математических преобразованиях, которые необходимо выполнить при таком предельном переходе. Поэтому сразу приведем итоговые формулы, которые являются основными соотношениями теории спектров. Они представляют собой пару преобразований Фурье, связывающих между собой две функции: вещественную функцию времени s(t) и комплексную функцию частоты G(w):

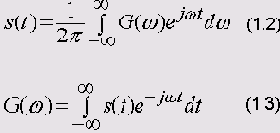
Формула (1.2) называется интегралом Фурье в комплексной форме. В данном случае предполагается, что функция непериодическая, поэтому она может быть представлена только суммой бесконечно большого числа бесконечно близких по частоте колебаний с бесконечно малыми амплитудами.
Если ряд Фурье представляет периодическую функцию суммой хотя и бесконечного числа синусоид, но с частотами, имеющими определенные дискретные значения, то интеграл Фурье представляет непериодическую функцию суммой синусоид и косинусоид с непрерывной последовательностью частот. Иногда говорят, что в .составе непериодического сигнала есть колебания всех частот. В случае непериодического сигнала говорить об амплитудах отдельных спектральных составляющих нет смысла, т. к. это бесконечно малые величины. На самом деле параметр G(w) выражает не непосредственно амплитуду, а так называемую спектральную плотность. Обычно эту деталь опускают и называют G(w) комплексным спектром непериодической функции, а абсолютное значение этой величины — просто спектром.
В специальной литературе можно найти теоремы, позволяющие облегчить спектральные преобразования сигналов, а также соотношения и графики, описывающие спектры сигналов различной формы.

Содержание Назад Вперед

Главная сайта